by B.B. Pelletier
Pyramyd AIR has is now putting polls on its home page in the upper left corner. If you haven’t voted on the most recent poll, feel free to do so. You can vote only once per computer.
Part 1
Part 2
Part 2/The budget rifles, continued
Part 3 The Olympic rifles
There’s been a LOT of interest in this series. I would judge that fully one-third of our readers are interested in 10-meter rifles, and we get a lot of new readers who find us through queries on 10-meter rifles. Today, I’d like to discuss what it’s like to shoot a modern 10-meter target rifle – one of the $3000 rifles we looked at in the last post.
What’s in the box?
The first thing you will notice is that a lot more stuff comes with your airgun than would come with a typical sporter. There are tools like Allen wrenches and an adapter to fill the removable air tanks. Typically, each new rifle comes with one or two air tanks. Except for Walther rifles, these tanks accept a fill to 200 bar. Walthers go to 300 bar.

Besides the fill adapter, there will be inserts for the front sight. Some modern rifles, like the FWB 70 and 700, have a front sight with an adjustable front diopter and don’t need inserts. Additionally, there may be adjustment blocks and accessories for the buttplate.
You will notice the weight when you lift the rifle. It will be in the neighborhood of 10.5 lbs. Also, when you lift the rifle to your shoulder, it should not fit. There are many adjustments to be made before you can call the gun your own. All of these are done in the standing position, not off a bench.
Adjustments
-
- Length of pull
- Height of cheekpiece – to locate sighting eye with rear aperture
- Location of cheekpiece (indented or out from the stock line) – to locate sighting eye with rear aperture
- Angle of cheekpiece (front in, rear out or vice versa) – to locate sighting eye with rear aperture
- Height of buttplate – to locate sighting eye with rear aperture
- Angle of buttplate (in toward shoulder or out & away from shoulder)
- Angle of pistol grip
- Location of pistol grip
- Location of trigger
- Angle of trigger
- Location of rear aperture sight
- Height of the forearm for aiming assistance
- Location of weights for balance
Once the rifle has been adjusted, it’ll fit like a glove. The weight you noticed at first will have diminished, but the forearm will still feel heavy. You’ll learn to hold your off hand close to your chest to make a platform to support the rifle’s weight. This is how you’ll adjust the height of the forearm – to the point that when the rifle is aiming directly at the target, you feel as though your skeleton and not your muscles are supporting the rifle.

The trigger is the first thing most airgunners want to adjust, but until the rifle is adjusted to fit you, the trigger adjustment is meaningless. A typical trigger-pull range is 30-60 grams, or about 1 to 2 oz. After adjusting the rifle to fit, you may want to adjust the trigger heavier – not lighter. The triggers of modern 10-meter rifles are two-stage with no weight in the first stage. The second stage breaks without the hint of creep, and an overtravel adjustment stops all trigger movement immediately after the break. At the lightest setting, about half the shooters cannot even feel the second stage engage and will fire the rifle unexpectedly.
The trigger also has a training function, or what we call a dry-fire feature. It can be cocked and fired with no effect on the rifle. I don’t know how much rifle shooters practice their triggers, but pistol shooters shoot about 5 practice shots for each live shot they shoot, and a good competitor will shoot a full match (60 shots for men, 40 for women) every day. This builds strength in the shooting arm as well as a feeling for when the trigger will break. Eventually, your subconscious mind will take control and start to break the trigger when the sight picture is ideal, which is the whole point of practice training.
Sights
The sights deserve a blog posting of their own, but some time back I promised to show what it looks like looking through these sights. There isn’t a camera I know of that can take that picture, so I’m showing you what the front sight looks like so you can make sense of the graphic that follows.

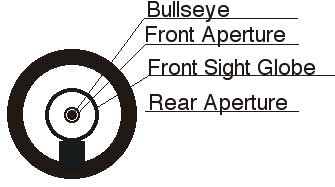
There must be a reason for the shooting jacket and pants. Is it to help maintain a good stance? Or is it a required uniform in order to compete?
Al in CT
Please stop this!!
Every post you have on these 10m guns puts me closer to spending a crazy amount of cash that should be going on food and shelter LOL
Al,
The jacket and pants do help hold the shooter in a rigid position. You can’t gain 10 pounds and still get into some of them!
B.B.
Dear LOL,
You’d better not read this blog for the rest of the week, because the next post is going to push you over the edge!
B.B.
B.B.
I’m surprised that top-level shooters pump their own guns. I would think that this would interrupt their concentration, increase their heartbeat, dilate their eyes and so on. How many shots per fill do they get?
How is SFC Parker’s left hand positioned? It looks like the fingers are pointing left, the heel of the hand to the right with the thumb on the right side of the stock. Pretty contorted.
Maybe it is one of the necessary life experiences to shoot a gun like this….
How do you pronounce 6-24X50 for scope size? Six to 24 by 50? I don’t want to sound ignorant when I’m shopping for scopes. Thanks.
Matt61
Matt61,
A tank gives 200-300 shots. They have several for their guns, so they don’t pump right before a match.
The hand is positioned as you see it. That’s why I mentioned his two world’s records. I try not to correct shooters who already have those.
Right, again, on the scope pronunciation.
B.B.
I’m loving this series!
Any idea why Pyramid doesn’t carry front aperture sight inserts (besides the Beeman kit, which isn’t for 10M shooting), and other precision sight parts? Before I embarked on making my own I was just going to order some.
I have my article on making the plastic front aperture sight inserts up as a web page now, let me know if you want the URL.
BB,
The P700 is going to take a while to justify, especially since I would have to buy a tank or pump and curtail my jet-setting:).
From the description of fitting adjustments, sounds like you tried one on and liked it. I know people are drooling at your description of the trigger, too. 1 to 2 ounces would be too light for me, though.
Thanks for the sight picture. Are the target and the front aperture in focus at the same time with the rear aperture somewhat de-focussed, or am I all wet?
I’ve seen that forearm grip before; it probably works better for some than others.
Hello all, on the subject of advanced technology and shooting, here is an anecdote from the field of archery. The specific area is the archery of Korean martial arts which apparently is the engine for the Koreans to dominate Olympic competition as they are doing in women’s pro golf, I understand, with their maniacal work ethic. I had a little taste of traditional Korean archery that involved an afternoon of lifting and drawing the bow with breath control. The word was that one wouldn’t see an arrow for at least a year, although that afternoon was enough for me.
Anyway, the story is that some Olympic archers with the latest equipment approached some archer monks for a contest. They blew the monks away at the targets, but the monks did not seem perturbed. They said now it was their turn and invited the Olympians to shoot with one leg hanging over a cliff. The monks retained their accuracy while the Olympians couldn’t hit anything….
Matt61
Felice,
Ten-meter inserts are a niche that a general retailer like Pyramyd AIR cannot stock. You should be looking at Neil Johnson’s website and Scott Pilkington’s website.
Hold your article for a bit. I’m about to announce a guest blogger segment and you could write it there, if that appeals to you.
B.B.
BG_Farmer,
Since you live in Kaintuck I must assume you will make the NRA Annual Meetings in Louisville in May. Pyramyd AIR will have a booth there and I’ll be there, too. You might get to see a 10-meter rifle, though I don’t know if they will bring one for sure. But it should be worth it.
The rear aperture is out of focus, but your eye seeks the brightest light, which is in the center of the hole. The darkness causes your pupil to dilate, giving you great depth of focus. So the front sight is sharp and the target nearly so.
B.B.
hi BB,
recently (a few days ago) I answered an advert on the internet about a second hand air rifle. It was a pcp and since I was looking for one (actually waiting until the discovery would ship to my country) I went to take a look. When I saw the rifle I knew this was something else than what I was used to. I own a gamo hunter 1250 and a gamo CFX but this..this was a daystate huntsman MK II PH6. The one with the six shot magazine system. Also when entering the serial number in the website I saw that it was the 40FPE version. This thing shoots like nothing I have shot before. really unbeleaveble. A real step forward :). NOW!! my question. For trying it out for the first time I rented a scuba bottle filled to 230 bar. (max of the bottle). Is this enough?? As I can see I am only getting about 20 shots (2 magazines) and then I have to refill. This way the pressure of the bottle is dropping FAST!!. would it be wise to swap the hammer spring for a 23FPE one? or will this be a waste of those mavelous 40 fpe??I know you own or have owned a daystate huntsman so I would like your advice. I’m really falling in love with this thing but it gets empty really fast 🙂 that’s the only drawback.Also, is 230 bar doable with a pump??… hope you can help me.. this is my first pcp 🙂
greetings from holland,,
BB,
Sounds good! I’m Nick BTW, Felice is my very understanding wife…
You can always email me:
nickandfelice@gmail.com
Nick
Holland,
You are dealing with the physics of fewer shots with greater power or more shots with less power. I would go with 23 foot-pounds, myself. Unless you are hunting big game, 23 foot-pounds is enough for anything.
230 bar is doable with the Hill pump and the AirForce pump. The FX and Axsor cannot go that high.
B.B.
Nick,
I knew you weren’t Felice, but I had forgotten your name. I’ll be in touch.
B.B.
B.B.,
Your comments about getting the gun adjusted so that the gun’s weight is supported by your skeleton, and not your muscles, spoke volumes.
Thanks for a great series!
Pestbgone
Pestbgone,
Just to be precise, I said it feels like it is supported that way. On shooters of my stature, the bones in the actual skeleton are quite far apart in this stance.
When we get over to 10 meter pistols, though, that isn’t the case. So we have developed an interesting hold that cantilevers our pistol arm to be a stronger support.
B.B.
BB, I’m sorry, but I disagree with the statement, “The darkness causes your pupil to dilate, giving you great depth of focus. So the front sight is sharp and the target nearly so.”
If your aperature (pupil) is large, then you have less depth of focus. This is basic in the field of photography (no, I’m not confusing depth of focus with depth of field). See https://en.wikipedia.org/wiki/Depth_of_focus.
B.B.,
Yes, I think I see what you mean, bracing myself against my own body and finding a sense of balance instead of fighting gravity. Gravity always beats me, so if I can avoid the fight I think I might get better results.
Thanks again,
Pestbgone
less depth of focus,
I’m no optometrist but i trust BB over Wikipedia any day. Were talking about focusing ones eyes to both the target and sight.
to Nick/Felice Luftschein
Please share your url for making the aperatures! I have an idea of how I might do this, but it never hurts to have other ideas!
It has inspired me to try that as a solution for my problem using traditional sights with my old eyes. I think perhaps this could work for my air pistols. It is really just a variation on the concept of Ring Sights isn’t it?
What do you say BB? Do you think this could help?
Thanks!
JBA
Looking through an aperture sight blocks stray light and only allows light parallel to the target to enter the eye, this causes an increase of the depth of field or focus. The rear aperture acts like the iris in a camera lens. You will also get the same effect in very bright light when the eyes iris closes down.
The 10 meter shooting stance is the same one I learned for shooting the 200 yd standing position in DCM service rifle and it does work very well. The only draw back was when I tried it shooting a Remington rolling block 45-70 BPCR at the 200 yd chickens. The stance was still steady but the recoil almost broke my back. After 10 shots I could feel what was in store for me later that day. You wouldnt think that a 485 gr. bullet going 1200 fps would kick that much more than a 168 gr at 2500. Maybe the gas recoil in the M1A helped more than I thought.
Sam
BB,
I probably won’t get to Louisville, but if I do I’ll look up the PA booth for sure.
Thanks for the clarification on the sight picture — I’ve used rear peeps in the past, but never in conjunction with a front aperture. Seems like the front aperture would make dealing with the bullseye a lot easier (than other front sight alternatives), since the eye will try to keep everything concentric.
My guess is somewhere between you and “anonymous” regarding the pupil dilation. I agree with you that it is in reaction to the restriction of light by the rear aperture, but I don’t believe it (dilation) could have any effect on the depth of focus, since the effective aperture of the system is likely the one in the rear sight aperture, assuming it is smaller that the pupil.
PS. Sam said it well (while I was writing)
Ahhh, yes. I was focusing (pun intended) on the statement about the dilation of the pupil. I should have looked at the total optical path. Dilation of the pupil won’t increase depth of focus, but as Sam & BG_Farmer pointed out, the effective aperature is the sight aperature which is small. This will give you better depth of focus.
BB,
That ring on the front sight looks floating in air, is that some kind of plastic with a circle printed on it? What is that post in the aperture sight?
DAvid
Depth of focus,
What I should have said is this – the tiny aperture blocks most of the light, just like the aperture in a camera. That causes your pupil to dilate, making your eye more sensitive to light – like increasing the ISO number for film. The result is an increased depth of field that allows you to see the front sight clearly and the target nearly so. The pupil dilation isn’t as important as the light reduction, except that it allows you to see the sight picture brightly.
B.B.
Sam,
Thank you for supplying the information that was missing in the aperture explanation.
A .45/70 recoils tremendously! If you shot with black powder, over half the weight of the powder, which is the remainder after combustion, must be added to the bullet weight to calculate recoil. I shoot a Trapdoor Springfield that kicks the hell out of me. I love shooting the gun because of the historical significance, but I really feel for the guys who had to shoot it in battle!
An M1 Garand is a pussycat, compared to the .45-70. But I can’t give either one up.
B.B.
David,
That particular aperture is an O-ring, pressed between two plastic plates that screw together. As you tighten the plates, the ring squashes and gets fatter, making the inner hole smaller. It’s an adjustable front aperture.
In the segment before this I showed a set of clear front inserts with different sized holes. In those, the sides of the hole reflect light, making the circle around the hole (which is really the wall of plastic material cut by the drill) look dark. A different way of achieving the same thing – a different-sized hole.
B.B.
JBA,
I’ve asked Nick to write a blog for this site, as a guest blogger. However, his URL is:
http://mechanicalphilosopher.blogspot.com/
No one has successfully created an aperture sight system for a handgun. Will you be the one?
B.B.
BB
That is a wonderful picture and diagram!
I have never used a peep sight, but would like to try it.
Could I put a sight system like this on the new Discovery? Are the front and back available from some place like Williams (with inserts or O-rings)? Is the post built into the back part?… Too many questions. A blog would be great!
Thanks
MCA
MCA,
If you already have the Discovery, see how easy the rear sight comes off. Crosman never gave me a rifle with this new type of sight, so I really don’t know if it does, but I think it should.
Then put a Williams or Mendoza peep on the back. You won’t get the sight picture shown in the blog. Your front sight will still be a square post. But it will be easier to see and use, which is why the military uses peep sights.
B.B.
All,
Can not say for sure why peep sights work better – even though I’ve read several reports on it over the years. Never the less they just do work better.
Thank you all for another wonderful blog. The pistol 10m blog offer lots of promise – can not wait.
Hopefully my Discovery 22 will ship in a few days.
DB
BB
I don’t have my Discovery yet. Like DB said, hopefully in a few days.
Williams has a wide variety – any recommendations (plinking, close range, low light, ageing eyes). If you are going to blog this topic I’ll gladly wait. Thanks
MCA
DB,
I like the phrase Mel Gibson used in t”The Patriot.” “Aim small, miss small.” A peep sight improves your aiming precision by enhancing the sensitivity of your eyes, but also by reducing the sight picture error. It’s like the pipper in a fighter pilot’s gunsite reticle. It makes it harder to miss.
B.B.
All,
On the peep sight issue – just remembered my grade school science.
Take a sheet of paper and punch a small hole in it with a ball point pen and then look through the hole. Your vision should improve. This works for most people; it works best if your near sighted. Different eye and light conditions require different hole sizes for best results.
Ok now while looking through the hole hold the ink pen up and pretend it is a gun sight move it way from your eye until it is clear and the target is also clear. Now while holding the pen still remove the paper and look at it again. Bet the ink pen and target are much more difficult to keep in focus. Try it is a simply test.
I read somewhere (years ago) that near sighted target shooters put tape on the lens of their glasses with small pin hole it to improve the sight to target picture.
Yes BB… aim small miss small… well sometimes.
DB
BB
Regarding my possibly inventing a workable aperature system for a handgun..
I will accept that challenge!
I somewhat doubt that I will “Invent” anything new, but perhaps Improved stands a chance???
Wish me luck!
The few ideas I have already had are the obvious ones that have also already been discounted for various reasons..
But.. you never know… maybe it takes a look at the problem from another angle. One without any preconcieved notions on how it “should” work.
Funny enough, I had done that in another job I had years ago. Engineers were working on a problem with a piece of equipment and I was aware of it, but never said anything untill it had been nearly 2 weeks and they were still hashing out solutions. I finally walked over, look over their shoulder and asked them to confirm if my suspicions about the nature of the problem were correct. They confirmed it, I left, came back 10 min. later with a sketch and said. “Have you tried this?” The look on the lead engineers face was priceless! He just said “Well… I think this will do it!” The solution was just too obvious for them to see it I guess! They couldn’t get a metal pin to drop into a slot on a nylon retainer due to the extreme speed of the retracting arm to be locked properly. They tried all sorts of mechanical dampers, electrical dampers, et. My solution was to cut a 45 degree notch in the leading side of the notch so the pin would have no choice but to not skip over the slot and would collide with the opposite (and higher) side of the notch.. The K.I.S.S principle in action.
I still find that one amusing.
JBA
JBA,
I have always suspected that sights will be the next major advancement in air pistols. A usable aperture could change the landscape of target shooting.
Go for it.
B.B.
Dear B.B.
My apologies for pulling this post out of the grave.
I live in the Netherlands and for some reason all the 10metre rifles are starting with a 1200,= euro clean ( about $1600,= a.t.m.) this is the rifle only and all are pcp some co2. No scubba tank, ore cartridges, ore fills.
First i don't want to win the Olympics with it, but i want a good accurate rifle that can compete with these. more to startle the "big" shooters with a cheap rifle.
Now i found a lot of modifications to ease up the Daisy Avanti 853. What i cant find is how accurate this rifle really is. only claims.
next with importing this rifle i only have a cost of less then 750,= euro's that is nearly half then the least expensive 10m rifle here to find.
Do you think/ know this rifle is that accurate ? ore do you maybe say go the extra mile and take the 888 for more consistency. and thus more accuracy.
(i prefer the 853 for the less hasle and filling test and technical tests it needs to enter )
Greatings
JD
Netherlands
Love the blog.
I've learned more here then on the range.
JD,
A Daisy 853 will group 10 shots from a rest at 10 meters onto the end of a pencil eraser. I make that about 3mm, center to center.
It's not quite good enough to shoot perfect scores, but close enough to do very well.
The main drawback is a long, hard (2 kilo) trigger that has a lot of creep. There are instructions on the internet about how to modify the trigger to around 750 grams with a lot less creep.
B.B.