by Tom Gaylord
Writing as B.B. Pelletier
This report covers:
- Review
- Today’s discussion
- Round balls
- Conical bullets
- Smokeless powder
- A big point
- Shape
- Round balls — again
- The bottom line
I’ve taken 11 months to return to this subject of ballistic coefficients (BC). That was in spite of some tremendous interest in Part 1 of this report last May.
I’m purposely avoiding all discussion of mathematics, which is difficult, since ballistics is a discipline that heavily employs mathematics. But I’m not qualified to write about the math; and, more importantly, I know that 99 percent of my readers would be turned off if I were to write the report that way.
Review
Last time we learned that the BC of a pellet:
• Is an extremely small decimal fraction compared to the BC of a conical bullet.
• Varies with the velocity of the pellet.
• Varies with the shape (form) of the pellet.
We also learned that the stated BC of a pellet can be forced to vary by where the measurements are taken.
We understand that diabolo pellets are designed to slow down rapidly in flight, and that the BC is a measure of the velocity retained in flight. So, a pellet’s BC rapidly changes over a short distance.
We learned that a pellet’s BC varies between 0.010 and 0.045. We also learned that pellets that have a relatively high BC (the larger numbers) will never slow down faster than pellets that have a relatively low BC. Even though all diabolo (wasp-waisted with a hollow tail) pellets rapidly slow down, the higher BC numbers are given to the pellets that slow down the least in relation to all diabolo pellets.
Today’s discussion
Today, we’ll look at the impact that shape (form) has on the BC. We’ll also look at the impact velocity has on the BC. Let’s begin with that.
Round balls
When firearms were first invented (we now believe that was in the 1300s), the earliest formal shape for missiles was either a shaft (arrow or dart) or a ball. The earliest projectiles were probably just stones, but that soon gave way to uniform lead projectiles that were easy to shape. Cannon balls were still chiseled from tough rock for many years before they, too, were cast from iron into spheres.
The round ball became more than just a projectile of choice. It became synonymous with the title — bullet. From some time in the 1400s to around 1840, the word bullet meant a round ball. Round balls are easy to enter into formulas and ballistics tables because the form is always the same. The weight varies, but not the form (shape). Because of this, the early science of ballistics was built around a spherical bullet, and everything was fine.
Conical bullets
Conical bullets (oddly referred to as conical balls in their early days) changed everything. Ballistics had to expand to adapt to these new projectiles. Several ballisticians worked out new formulas to account for the different new forms, but by now the forms were changing faster than the science could keep up.
Smokeless powder
Then, smokeless gunpowder came on the scene and things changed again. Velocities with black powder (which, up to that time was just called gunpowder) topped out somewhere around 1,600 f.p.s. Within 20 years, smokeless power doubled that speed; and in another decade, it added another thousand f.p.s. Suddenly, bullet makers had to be concerned with shapes that flew at ultrasonic velocity. This was decades before anything else approached that speed, so things like wind tunnels weren’t even available for modeling.
It may seem like I’m getting far from the topic, but here’s why I am telling you this. In 1870, the Rev. Francis A. Bashforth — the inventor of the first (?) electronic chronograph — discovered that drag increases with the square of the velocity at speeds between 430 f.p.s and 830 f.p.s. — but with the cube of velocity at speeds between 830 f.p.s. and 1,000 f.p.s.! That higher range is the trans-sonic region that we tell airgunners to be wary of. We used to think it caused inaccuracy, but I disproved that in 2011 in an 11-part blog series titled Velocity versus accuracy. But what it definitely does do is increase the rate at which projectiles slow down.
I could easily get into a discussion of the ideal shape for supersonic projectiles, and there are many airgunners who would like that. “Just design a solid pellet that has a boattail, and all your problems are solved,” they say. Yes, all problems are solved, save one — accuracy. No airgun I know of is capable of accurately shooting those solid pellets (that I’ll now call bullets) at supersonic speeds. In fact, very few airguns can get them up to supersonic speeds at all! So, the discussion is over before it begins.
A big point
If something can’t be done, it makes very little sense complaining about what “they” should do. The blog readers know that I’m not a negative person. I’m willing to try anything that has a chance of success. But physics is physics! I’ve learned in all my experiments and reading that airguns have practical velocity limits. We may not be at the limit today, but we’re very close. Because, to push a pellet any faster than about 1,500 f.p.s. (1,486 f.p.s. is the fastest pellet I’ve ever observed), requires us to do things with compressed air that it just doesn’t want to do. The speed of sound governs how fast air can flow. Pellets can be pushed faster than the speed of sound; but to go much beyond 1,500 f.p.s., we’re going to have to use a different compressed gas.
So, pellets that top 1,000 f.p.s. are slowing down at least at the cube of their velocity. That’s what Bashforth tells us. Take another look at the chart I showed you in Part 1:
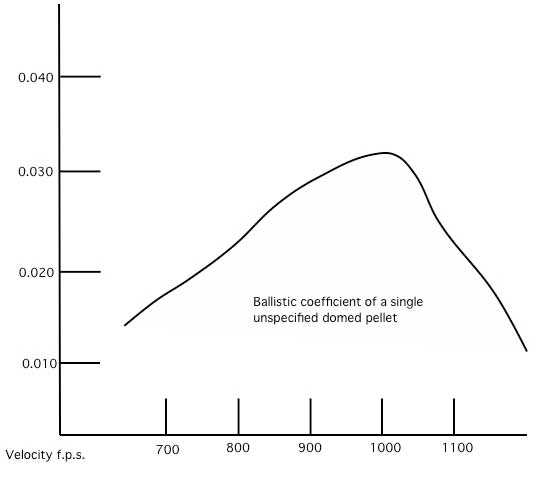
This is how velocity affects a hypothetical heavy domed pellet.
The chart isn’t real, which means it wasn’t generated by actual test data, but the relationship of the BC decline at the trans-sonic region is representative. Lighter pellets fall off their BC at lower velocities, so take the entire curve and move it to the left. The same thing happens — just at lower velocities. Heavier pellets fall off at higher velocities, too. But all of them fall off in the same way.
Shape
Enough talk about velocity; now let’s look at what the shape (form) of a pellet does to the BC. Just as certain shapes work well at supersonic speeds, there are also good shapes for subsonic speeds, where most pellets live. A domed nose with a solid cylindrical body is very good at subsonic speeds. And the more it weighs, the higher the BC will be.

The shape or form of the pellet has a lot to do with the ballistic coefficient.
The wadcutter, by contrast, is the worst shape — or at least it’s down there withe the worst of them. Some people feel that hollowpoint pellets are even worse because their hollow points act like air brakes. Others believe the hollows fill with air under pressure, and the pellets then act like wadcutters.
The pointed pellet is not as aerodynamic as its shape seems. While it looks sleeker than a dome, it doesn’t turn out to work that way at subsonic pellet velocities. A point is great for supersonic speed, but it does very little below the speed of sound. Pointed pellets do penetrate deeper in solid media; but in the air, they aren’t that different from domes.
Round balls — again
Round balls — remember them? As it turns out, a round ball is sleeker at subsonic velocities than any diabolo pellet. Only when the pellet weighs considerably more than a ball of the same caliber (and may be too heavy to shoot effectively) will it have a superior BC. Round ball BCs hover around the 0.07 mark. That’s about double what the best diabolo pellet offers and several times what the average diabolo has.
So, why not just shoot round balls? Simple answer — accuracy. Round balls don’t have any accuracy at longer distances. The high drag of the diabolo pellet — the very thing that destroys their BC — is also what helps them be so accurate.
The bottom line
Yes, the BC of a pellet is important, but only after you know that it’s accurate. If you can’t hit what you’re shooting at, the retained velocity of your pellet means nothing.
So, search for accuracy first and a high BC second. Or, in some cases, such as long-distance hunting, look among the pellets with high BC numbers for the one that’s the most accurate. Don’t just shop for the highest BC unless you also understand the relationship of your gun to that number (re-read Part 1 to understand).
Is that all there is? Of course not. We could go on and talk in more detail about form, but I think the basics have been covered.
I know that many of you use the Chairgun program and find it very useful. One of the things Chairgun requires is the input of the BC of the pellet in question. Sometimes, you only discover how close that BC is after shooting your gun and matching the results to the Chairgun predictions.
I don’t know if I’ve helped you understand ballistic coefficients or if I’ve just confused you more. If you remember the basic things I’ve outlined in this report, it’ll stand you in good stead in your future shooting.

LOOKS? Or! Seems like we’ll have all weekend to chew on this one? Semper fi!
No time to read todays blog in detail…perhaps a bit more over the weekend, but…
Funny thing happened this past week…
Took the Air Arms S510…Wait, no, the FABULOUS S510 FAC in .177… precharged to its max and cranked off a series of full powered pops with the B. B. recommended Crosman “Lite” pellets and…”WHACK!” “WHACK” (etc, etc, etc.).
Supersonic manifestation to the suprising level that the Rangemaster cautioned “No rapid fire on the civilian range” (Probably the first time referring to an air-gun there, ever.)
Interesting, since it hadn’t happened before. Usually it pops (tops) out, at full power, at the more ragged edge of supersonic with more a “Thuptupt” report, like it wants to exceed that sound barrier thing but can’t quite make it.
But today, “WHACK!”
Air Arms Suppressor at work and all, I figure, for the good.
But the more I think about it, the more it harkens back to those days of yore, (trying to) quiet down the M14. One can maybe affect the gun but the environment/weather will cheerfully modify sonic-boomology to suit itself, not particularily you.
Since round balls are out because they are inaccurate, and since domed pellets are always the most accurate and have the highest BC vs pointed pellets and hollow points, it would seem that shooting anything but domed pellets is a waste of time.
John,
It’s not black and white. If you shoot targets, for example, only wadcutters work well. In fact they are the only type pellet that is permitted in formal matches.
Hollowpoints have their uses at close distances for hunters.
Only the pointed pellet seems to be wanting.
B.B.
B.B.,
Are you referring to 10 meter matches or other distances as well regarding the required use of wadcutters? I’m pretty sure you mean 10 meter matches only. However, I will have to let my ignorance shine here. I had no idea that wadcutters were required. It makes sense when you take measuring into account. But I didn’t know they were mandatory. But then I have never shot in a 10 meter match either.
G&G
G&G
G&G ,
10-meter matches.
B.B.
BB
I’ve been experimenting with pellet samplers with my new 2400KT. So far it has liked JSB Stratons, a pointed pellet, the best. PA does not appear to carry this pellet in 177. How about suggesting that they carry it.
Hope you enjoy the show at Melvern,
Jim
G’day BB,
Remember the old physics one. What hits the ground first? A bullet dropped from 3 feet or the same one fired absolutely level at 3 feet at xxxx FPS.
Cheers Bob
Unless you have a projectile with a trajectory long enough for the curvature of the earth to be significant… No difference.
BB,
I know this may cause some confusion with some newbies and I do apologize for this, but just to make sure my head is on straight, one of the reasons that round balls are not accurate in an air rifle is because the twist rate of the rifling is all wrong for them, is that not so? If we were to use a barrel with a twist rate of say 1:45 or slower, would not round ball produce better results? I know muzzle loaders can be surprisingly accurate at considerable ranges.
RR,
No. In fact, the 1:16″ airgun twist rate isn’t bad for round balls.
Round balls are simply not as accurate at longer distances as conical bullets, or diabolo pellets.
Remember my Nelson Lewis combination gun? As good as it is, it cannot keep up with rifles like my Ballard. Round balls are for close ranges of under 200 yards, and really for 100 yards and less. In airguns that drops back to 20 yards, or so.
Try some yourself and see what I mean.
B.B.
BB,
Then why do most muzzle loaders have a much slower twist rate? I have had several flint lockers recommend that I go with a 1:66.
Golly gee whiz I wish I could afford to have a gunsmith make me some barrels!
RR,
The larger the diameter of the ball, the slower it needs to spin to stabilize. The earth spins once every 24 hours.
B.B.
While a bit short on time at the moment, I believe that B.C. calculation involves checking pellet speed at point of impact, thus putting your chrony downrange, then,…comparing that to the pellet speed at muzzle. Caution, pre-cautions and confidence required.
I do not think that mathamatical discussions are bad. We have calculators and computers. Plus, think of what kids are learning (we hope) at younger and younger ages. And, many things can be explained in very complicated terms or very simplistic terms,….just a matter of finding that happy balance.
Chris, USA,
I for one am very concerned with what our kids are learning at younger and younger ages. That is why my grandson is in a private Christian school.
As for the mathematical discussions, I think what BB was wanting to do here is to give a good general overview of the subject that would be very easy to understand, most especially for those who are new to air guns, without overwhelming them. If he jumped into all of the calculations, this would be the subject of 10 or 15 blogs. After a bit of that, I would just turn the computer off, pick up my air rifle and go shoot.
RR,
You got it! I think I would turn my computer off while writing such a blog. 😉
B.B.
RR and Chris, USA
Its not only at younger ages as I think this short video will shock you as these are college students that will soon be the leaders and be voting to shape the country of the future.
http://safeshare.tv/w/oHbxeOtsOP
We are in trouble
BD
BD,
That is pretty sad, but I am certain that our parents and grandparents said the same thing about us.
Often we wish to be a teenager again with the knowledge and wisdom we have now. I am not so sure that would be a good thing. Although such could help us to avoid many of the pitfalls we have experienced, which shaped the person we are now, it could also lead us down paths we should not tread.
RR
I myself do not agree that my parent or grandparents said that about me as I was a very head strong and independent child as I was out hunting with a 12 ga shotgun that I bought with my own money from cutting grass at the age of 8 years old by myself with my father permission as well were four of my other friends. We camped out on the islands of Cocoa beach Florida every weekend during junior high and ate what we killed while camping.
By junior high I could have answered every one of those questions without hesitation and was riding and fixing my own dirt bikes at 14 years old so I do not agree as in my youth we were actually taught the truth about this countries history and given a much more thorough and well rounded education than what is being taught to our children today.
We said the pledge of allegiance every day and true patriotism was part of our everyday life instead of it being shunned and removed from the schools standard procedures as it is today.
There was never a word said about wearing a shirt with the American flag on it as it was actually encouraged.
I have wished I could turn back the hands of time many many times knowing what I know now as I would have done many thing very different indeed and do not believe that they would have been wrong choices as I made some of those anyway but managed to solve and survive despite the stupidity of my ways. My most definite thing I would have changed would be to buy as much Microsoft and IBM stock as I could have afforded to in 1985 so I would be one of the multi billionaires that are ruining this country today since the y think that money can rules the world and gives them the right to decide how and what we should have to live with or without only I would be their rivals as I would be fighting for the country I grew up in to be brought back rather than be destroyed as they are doing now.
BD
Buldawg76,
I agree with much of what you have said the last couple of days. GF mentioned when I first came on here, it’s best to try and avoid politics. Mine is a general feeling of disgust with the whole lot of ’em. That’s all I will say.
Was going to respond below, but no room. How’s the Feild Target coming along? Top of the class yet? One video I saw had people walking through the woods to different “stations”, doing the diff. positions. Then another was at a range where they pretty well stayed in one place, Which type does your club do? The woods/stations type sounds more fun.
RR
I agree with you as far as politics go as well but then if us older folks don’t get the younger minds questioning the things that are happening in DC right now things will never improve for them and I just believe that it has to be done by every source that’s is available as they will not hear the truth from the newspapers or evening news on TV and most definitely not on any political dedicated news channel as those are just telling them what DC allows them to say since our first amendment is merely a joke anymore now that the govt has it censored to the point that they can only report what DC approves as there have been numerous reporters fired for not being willing to conform and tell it like it is. that is my main and only goal with what I say as it has to start somewhere or the country we leave for them will be another Russia or China.
We shoot the Ft matches in the woods where you are walking up and down hills and shooting down in hollows , up hill side and also some target are in a tree limbs 30 plus feet off the ground so it is just the same as if you would be out in the woods hunting. there are anywhere from 10 station to 20 station depending on the number of shooters so we are not holding each other up or having to be rushed to get each station done. There are two targets per station and two shots per target. when we hold AAFTA sanctioned matches there is a 5 minute time limit per station to make the 4 shots but we were supposed to be having one the 16th and 17th of may with it being a 50 shot per day match but our president has some health issues that has required him to be hospitalized so it was cancelled for now. I hope we have when he is better as I was looking forward to it and no I am nowhere near the top yet but am improving my score each match so as long as I hit more targets each match then I am happy as I cannot compete with some of our member that are shooting in the WTFT open class with 8000 dollars in their gun and scopes.
BD
Buldawg76,
Glad to hear from you. Hopefully your match will be back on soon. Very cool, sounds fun. 8000$,…wow. I did not realize that you could get that much wrapped up in an airgun and scope.
Curious, do they allow spectators?….as you would see in a golf tournament?
See at bottom for the Hatsan comment. Chris
Chris, USA
Yea I hope it will be back on soon as well. when you have a Steyr competition air gun and a March scope it is very easy to get 8000 plus in an air gun. there are three guy in our club that have very high dollar equipment but have been shooting for years and attend national matches.
yes spectators are welcomed as I went last October when we held the national’s at our range and there were shooters from as far as Venezuela and Puerto Rico in attendance.
BD
I”‘ve gotta couple do-overseas on my wishlist!
Overs becomes overseas?
What’s supposed to be so smart about these phones again?
RR,
While I am not qualified to comment on what kids are, or, are not learning, I can say that I am not impressed with “youngins'” we have hired right out of school. Academics aside, a stong work ethic, or any at all for that matter, seems to be the most lacking. Of course, there is exceptions to that statement.
As for math, I agree with your statement. When I get into something, I like to learn and understand all I can. That is just me. I don’t always get it, but I try.
Chris,
Please do not take the following rant of mine to be in any way critical of you. That is not my intent. I am just in the mood to rant for a bit.
There is absolutely nothing wrong with wanting to know more. I too like to dig deeper. What BB is trying to do here though is touch on many things, some of which you could literally devote your life to researching, this blog’s subject being one of them.
He also helps us sort through all of the gobblty gook marketeering hype by doing some remarkably in depth reviews of as many airguns as he can, saving us a lot of money by not having to learn this stuff on our own. He has helped me to avoid several heartaches over the years and also to pick up several darlings at some great prices.
Each one of us have different tastes, such as I have no use for CO2, but I am obsessed with long range accuracy. Others like collecting replicas or antiques. Some want to hunt. Others just want to plink. BB tries to give all of these different tastes some of what they desire with this blog. That means one day he is reviewing a Wacko Backyard Poofer and the next day a Humdinger Hawg Whacker 2000.
More often than not, when there is a subject that he feels we or he himself would like to give more time to, he will post it on a Friday. Then we will have all weekend to chew on it and exchange views, knowledge, etc. We and he have the chance to expand our learning and even friendships at a more leisurely pace with the opportunity to give more thought to the subject.
If there is a subject we would like him to enlighten us on or would like a more in depth look at, he often obliges us or if he feels it would take too much time, he often points us to where we can find what we are looking for on our own.
I’m done ranting for the moment. Now turn off the computer and go outside and shoot your airgun some. 😉
RR,
No offense taken. Your comment is right on point. Yup,..BB and this sight is great.
“Backyard Poofer” and “Hawg Wacker” sums it up well. BB serves it ALL up!
And yes, spend some time here, and you will learn how to spend your hard earned money well, whatever your “taste” may be.
RidgeRunner,
In a few hours I will be going to the airgun show in Malvern, Arkansas. I think back on those times at the Moose Lodge in Virginia when Mac and I were at the airgun show, and I think what a shame that show is no longer running.
You never saw that show when Fred Liady ran it at the Civic Center in Roanoke, did you? He had up to 120 tables at his show and at the time it was the biggest, most active airgun show in the world. It was something to see.
I hope to grow the Texas show even larger some day. This year we will probably have in excess of 80 tables and 500 people through the door. The attendance would make our show the largest, ever, if we hit that number. We were slightly over 400 through the door last year, and that was the first year the show ran.
When a show gains that kind of momentum there is no telling what you will find. I once saw $46,000 change hands over 3 BB guns in the aisles of the Roanoke show. And I saw and handled a military Girardoni rifle that sold for only $3,500 a year later. Such a rifle is now worth in excess of $75,000 on its own.
I hope someday you are able to attend a real active airgun show, so you can see what I have been talking about all these years.
B.B.
B.B.,
Please wish the same for me. I would love to make it to several good airgun shows. I think the closest to me is in Western N. Carolina which would be roughly a 10-12 hr. drive. Too much for my health. I love collecting and airguns are obviously very appropriate for me. Right now the only airguns I collect are the replica guns.
By the way. Is there anything in Atlanta?
G&G
BB,
I did indeed attend several of Fred’s shows. I started attending his shows in 2005.
I first met you at the 2008 show. I had discovered your blog that year and I made it a point to hunt you down and meet you. You had two Turkish copies of the Gamo CFX for sale. That was the show where I bought my CFX. If I am not mistaken, it was Fred’s last show.
The next show I think was his memorial show. I believe it was the show that Mac brought you to just after your illness. That show I bought my Izzy and asked your advice on what to feed it. Mac kept urging me to buy that NIB Diana 75. If I had had the money, I would have.
I am hoping the Hickory, NC show will grow into something.
Alexander Forsythe, Francis Bashforth; which clergyman will make the next great firearm invention?
Fishmonger,
You know what I’m thinking the same and you’re just saying it. Forsythe invented the percussion principal but I didn’t know about the chrono inventor!
Errol
Sorry I meant principle.
Errol
What do you want, good grammer or good taste?
If we want to see BC, check out EunJin .177 16.1 grain pellets. I bought them just for my collection. I do not have an air rifle that could shot them..Lol..
Pete
Hi BB, I envy you going to the show.I think todays blog brought up an
interesting debate about the different types of pellets.I have been using
round balls in some of my tight loading guns since my RA limits me loading
but I use the domes most of the time
Going off track for a while,I am considering the Freedom Eight Compressor
because the hand pump is getting to hard to use.
It seems ok and I know you must use a small shop compressor to help fill
it.What do you think about it” I found it is the lowest cost in my budget for now.
Michael,
I consider my air compressor to be the best one on the market and also one of the best purchases I have made in years.
B.B.
Well I went back and read part 1. All of it.
A lot of things were talked about. There is something we was talking about the other day on the blog which is related to today’s blog. The balance of the pellet. Where the center of gravity is located on the body of the pellet.
In other words if we could set the side of the pellet on a point of a tooth pick or something so we could tell how much of the body of the pellet is ahead of or behind the center of the pellet.
Im pretty sure that if that balance point would be moved forward or backwards on the pellet it would affect the way the pellet fly’s.
Maybe that would be related more to accuracy of the pellet. If the pellet would be more likely to go off course if the balance point was wrong. Or maybe I should say less ideal.
I watched the American Airguner last night and BB was talking about pellet velocity verses weight and accuracy and he used the Wiscomb if I spelled the name of the gun right. And BB mentioned how the harmonics of the barrel could be adjusted with a movable brake on the end of the gun. And that was a reason to help the pellet fly better.
Then some body there asked how you could accomplish that with a gun that doesn’t have the options that the Wiscomb has. And I believe Rossi said if I remember right that it again boils down to find the right pellet for your gun.
I think there is a lot of little mysterious features that pellets have that are not seen that make a difference in the way the pellet fly’s.
And maybe that’s the reasonable round balls don’t work as good in some guns. How do you change the balance position of a round ball?
Gunfun1,
I am very surprised that you have not already threaded a solid barrel or shroud,.. and..add a weight,.. in an effort to “tune” barrel harmonics. Really,…you have the tools at hand to do so.
Chris, USA
I have used the barrel band clamps on Crosman and Benjamin guns to position at different places on the barrel. Like the ones that come on the Benjamin Discovery’s.
What I have found is some guns it helps and some it doesn’t make enough difference to worry about it.
And I don’t know if you noticed. Some pcp barrels free float if we should call it that. Some guns have the barrel extending right out of the breech with no support or clamp if you will the whole distance of the barrel. Even some guns that have shrouds like the Marauders are free floating the whole distance from the breech to the tip of the muzzle. The clamp that you see at the muzzle of the Marauder barrel is basically just a gaurd. It does not contact the shroud. Or I should say shouldn’t contact the shroud.
So I guess it all comes down to that one saying. One persons acceptable accuracy may not be the same as another persons.
All I say is go shoot and have fun. Experiment with things and learn is the best advice I can give for these airguns.
Gunfun1,
Yes, I have noted some PCP barrels are “floated”. I was not aware the Marauder was. Still looking and learning, but the .25 Marauder might be on the list. Price is good and leaves room for a pump and tank.
While I have not checked it out, I would not be surprised that someone has not taken a Hill pump, mounted it, motor, belt, fly wheel. etc., and automated it. Limiting pumps per minute seems like it would be the only factor. Maybe an alternative to a shoebox pump?
Chris, USA
Yep there is video’s of people doing that to the hand pumps.
I actually thought about making one before I got the Shoebox.
The Marauder “barrel” is not… The Shroud is free from receiver to muzzle… But as I recall, the baffles inside the shroud press against the muzzle end of the real barrel.
Wulfraed
Nope. The barrel and shroud are a assembly at the breech.
There is a plastic deal at the muzzle end of the barrel that supports the inside diameter of the shroud.
Nothing supports the barrel or shroud at the muzzle end. Thus the barrel and shroud fliats.
You can remove the barrel band out at the fill fitting and the barrel and shroud contacts nothing but the breech.
The barrel and shroud definatly float as a assembly.
Should say.
Thus the barrel and shroud floats.
Not floats. Whatever the heck my phone thinks that word means.
Man can’t even correct my phone right.
fliats
fliats
fliats
That is the wrong word!
Gunfun
The principles you are talking about her as far as the center of mass of the pellets are exactly the same thing that Burt Munro had to figure out and use in his Indian motorcycle to run it at the Bonneville salt flats back in the late fifties since it would start to head shake at speeds above 150 mph and he played with adding weight on the bike in a forward or rearward position until the weight bias was just right that it allowed him to set the worlds land speed record for a 1924 Indian Scout streamlined twin cylinder pushrod engine of 201 mph.
That record still stand today as far as I am aware of and there was a movie of his life and him ruining at Bonneville called the ” Worlds fastest Indian ” and in the book it tells of when he passed that Ed Iskyderian of Isky camshaft fame bought that motorcycle to examine the cam that he had hand ground in his garage on a bench grinder and hand files as well as casting his own pistons and numerous other parts. Ed Iskyderian after examining the cam and its profiles stated that the bike should have not even run much less been able to do 201 mph.
Burt Munro was not an engineer or had any schooling other than a high school and yet he built and designed a bike that broke a record that still stand today.
BD
Buldawg
With you on all you just said.
And all those old hot rodders are my hero’s.
Comic books were cool when I was a kid. But give me a Hot Rod magazine and you wouldn’t see me for days.
I was so into cars that’s all I thought about. It was just some kind of passion that burned hard deep down inside me. I wanted to know and learn everything I could about making a car beat somebody else’s car.
And it wasn’t about beating the other car so much. It was ab out feeling I accomplished something.
And I do airguns the same way.
Gunfun
Yep the exact same way only I was doing it with bikes and cars but was more of a street racer than at the drag strip. We would go and race at the strips on the run what you brung nights at times but it was mainly on the street.
Yea the old timer were my hero’s as well like Smokey Yunick , Don Gartlits, burt monro and Max Buchowski of the Old Yeller Fame.
It was most definitely more about your own accomplishment than beating the other guy but beating him was just the icing on the cake. I built a 175 Yamaha dirt bike that would out run any 250 in town and most 360 as well and they always wanted to know my secrets but I would just smile and tell them to do their homework and they would figure it out.
Same with air gun now just as you.
BD
Buldawg
Yep.
🙂
Hi B.B.
Thank you Sir. I had just this subject on my mind & theres an entire blog on the subject. I do believe you are telepathic, as this is the third time!!
Errol
Errol,
I am indeed telepathetic. Just ask Edith.
B.B.
B.B.,
Really? You’re telePATHETIC? 🙂
TelePATHIC…well, sometimes.
PathETIC? Well, sometimes 🙂
Dyslexic? Usually! 🙂
Edith
You tell him Edith!
Yes, our wives expect us to read their minds, but we usually fail miserably. I personally think that is intentional so as to keep us off balance and groveling for forgiveness.
Edith,
🙂 What’s left to say? On a side note, I have been on some “other” sites in search of PCP info. and products. One thing I can say is,….the P.A. site is by far the easiset to use, most informative, detailed, easy to navigate, go in, back out, hop around, back to top, linked, etc., etc., etc. ….
“Hat’s off” to the team behind it !!! VERY well done.
Chris
Interesting to think about pellet stability.
I have always thought of BC as a theoretical expression of the “efficiency” of the projectile at a reference velocity (sort of like an aspect ratio) that looked at the frontal area, length and form/drag of the projectile and provided a “number” that would indicate how well/poorly a projectile would retain its velocity/energy.
I say “theoretical” because in the real world the energy and forces acting on a ballistic projectile are constantly changing so predicting the trajectory could only be done by a powerful computer or lots of practice to develop a good “gut feel” of where the impact will be.
So… with our diabolo pellets we have a hollow skirt and a solid head that will give us a forward balanced projectile that is directionally stabilized because the center of gravity is ahead of the center of pressure and additionally we have a drag-component that helps to keep the oriented on the flight path.
Thinking aloud… considering that the round ball has the best BC and that it suffers from poor accuracy because it lacks directional stability (its easily influenced by outside forces) it seems that the pellet designers adding pointy brass and plastic thingies to the front of the pellet should really be looking at adding a streamlining cone with stabilizing fins to the back of the pellet.
I think I am just going to go outside and do some shooting. 🙂
Vana2
Vana2
I think the C.G. plays a big role in the flight of the pellet.
And I just got me a new thumbhole wood stock Hw97k in .22 caliber yesterday. Trew the Hawke sidewinder scope on it last night. And I was out shooting and zeroing it in this morning but its windy as can be.
I wonder if I had some stabilizing fins on my pellets if I could get some better groups in the wind. 😉
a new HW97K – NICE!!! You seem to have a preference for the .22 caliber, is that for hunting reasons?
Been really windy here of late – tree-toppling, branch-breaking windy! Not good for shooting at all!
Fins might cause “weather-cocking” on the pellet – maybe a bit of propellant in the skirt would help. Best just to turn down the wind – let me know if you figure out how to do that! 🙂
Good weekend eh!
Vana2
Vana2
No I don’t prefer .22 caliber. I actually prefer .25 caliber. And I do like .177 caliber. All 3 calibers have their advantages and disadvantages. I’m not going to get into all of that right now though other than saying one needs to choose the proper tool for the job at hand.
And Buldawg just sent me that little article you sent him about them slow crawling 4 legged creatures. All I can say is excellent and dead on in every account. I saved that to my favorites. I think that’s as far as I will go here on the blog about it.
Vana2
Oh and yes the 97. That happened because a gun I had wasn’t working out like it was suppose to. Let’s say it was having technical difficulties.
So it was about out of warrenty and I traded down to the 97. And it was another airgun place that I won’t say. But I will say they did give me a good deal.
I’m kind of getting me a little collection of underlever fixed barrel springers. And almost got a.25 caliber version but haven’t had good luck with .25 caliber springers and nitro guns. So decided for .22 caliber since the charteristics of the 97 resembled the .22 caliber LGU I have. The Tx is .177 caliber and tuned. Its my field target gun or should I say my mini-sniping gun.
But I like .25 caliber pcp guns. And if you ain’t shot one yet that’s turning out around a 1000 fps with a 32 grain pellet. Well you should. I think you would like it. I do. 🙂
How ’bout we talk calibers later. I feel the pull of the dark-side… a .25 is calling! (but which one?)
Yes, four legged creatures. Glad you liked it!
Vana2
Vana2
Read below my reply to you and Chris about .25 caliber pcp guns.
Gunfun1,
I would be interested in hearing your thoughts on .25 PCP selections as well. Actually, anyone interested in a .25 PCP would probably appreciate your thoughts.
Chris, USA and Vana2
Ok my thoughts about a.25 caliber pcp’s.
Magic words my thoughts. Other people I’m sure will have their thoughts also.
But to me a .25 caliber pcp gun is kind of a all purpose gun.
They definatly can hunt. They can target shoot good. They can stretch out their legs as I say at longer distances than some air guns and still retain good hitting energy at distance. Definatly have the fun factor to them when plinking. In other words they will wallup the heck out of a pesky ferral can..
And again my opinion. So if anybody feels a different way about them please say what you exsperianced. And again exsperiances make the difference. Not what ifs.
Chris, USA and Vana2
Oh it looks like you mean what brand .25 caliber pcp to get.
Well that’s a easy one. Whatever brand you prefer. There’s numerous manufacture’s out there that are making .25 caliber guns.
The only brand pcp guns I can say about is the ones I have owned which is the Marauder and a AirForce Talon SS.
But I have owned a few nitro piston .25’s and can say I didn’t like them. To hard to control and not very accurate out past 30 yards. And that’s pushing it on distance.
And again my exsperiance.
Gunfun1,
Yes,…brands. Do appreciate you sticking to the “facts” though. The AF line has my interest, but no repeaters for the Talon, Escape and Condor lines. The high scope rails disturb me though. They must have a bit of a forward slant built in? They almost have to.
While your at it, “speculations” and “wish list” .25 PCP’s are welcome. 😉
Oh,..and yeah,…no price limit!
Chris, USA
Same thoughts about the high scope mounting for me with the AirForce guns. That’s the biggest reason I don’t have my Talon SS anymore.
And a .25 caliber wish list for me. Got mine already. The Marauder.
And I want a nice functioning true semi-auto action.25 caliber pcp. I want the action to work off of air. The FX Monsoon design is close to what I want. But not quite the way I would like it.
And me and Buldawg just texted back and forth about a few ideas I had about a semi-auto gun. I could very easily machine a breech block that would contain the trigger and valve that i talked to Buldawg .about.
It is something I’m very strongly thinking about doing in the near future. But already got in my mind how it will work.
Gunfun1,
Posted, but no show. Checked out the FX Monsoons,..very nice! (I give Vana credit for that). And,.. true semi-auto unless mistaken. In fact, true semi’s seem quite rare.
You almost got me sold on the Marauder. Still looking though.
Homemade semi adapter,.. now that IS interesting.
Chris, USA
Not a dadapter.
I want to make my own gun.
Chris, USA
Yea we have been throwing ideas at each other about a semi auto PCP gun that use only the air in the cylinder to shoot the pellet as well as cycle the magazine for the next shot and be able to do so fast as you can pull the trigger and use the least amount of air per shot so the shot count will still be as close to most quality PCP gun available for purchase today.
It will be a very simple yet effective design.
BD
Vana2,
BB did not want to get into the math but you are right: the BC is indeed a numeric expression of the performance of a projectile in relation to a “standard” projectile and is affected by velocity, air density, humidity, etc. Published BCs are usually normalized to standard atmospheric conditions to make comparisons meaningful.
A more basic number is the “coefficient of form” which relates to the efficiency of the projectile’s form ignoring the mass. Two bullets (or pellets) with the same coefficient of form will have BCs directly proportional to their relative weights.
If you have Colonel Hatcher’s Notebook he goes into detail on the different “standard” projectiles that were used in developing ballistic tables. All of this is an attempt to mathematically model projective behavior and none of them are perfect are good enough for most people’s needs.
Paul in Liberty County
Hi Paul,
Thanks for the details!
Will have to see if I can get Colonel Hatcher’s Notebook – sounds like an interesting read.
Vana2
Woke up with a splitting headache this morning but I’ll be rereading things all weekend.I missed the first part so I guess I should start there.
Reb
Yes read part one first.
B.B.,
I find this information about ballistic coefficients very interesting but I certainly hope that where you will eventually lead us in this series of blogs is the practical application of this info. Right now the practical use of the ballistic coefficient of a pellet does elude me. Actually, it seems that other than knowing what that number is there isn’t much one can do about it. Once you find the most accurate pellet for a rifle the B.C. simply is what it is.
But, I know there has to be more to it than that. I am counting on you to teach me and I know you will as always, I just have to be patient. Thanks.
G&G
For the most part, the BC will affect the trajectory, and thereby the effective “point blank range” (that set of distances for which one does not worry about hold-over or under) for a given zero.
10m competition aims (no pun intended) for a “kill zone” of 0″, and a PBR of exactly 10m — so any trajectory is acceptable as one can adjust the sights to zero at that one distance. BC is ignored.
For a small game or pest gun, having a long PBR (say a +/- 0.5″ hit range, aka a 1″ kill zone) would allow holding dead-center from, say, 25 to 40 yards — no need to compensate via hold-over/under. Higher BC (while remaining accurate) is better.
I’ve found some very odd things chronographing downrange, from one waisted pellet to another, to the extent that the pellet with the highest muzzle energy may not retain that advantage at all past 30 yards, and that 22 pellets against all odds barely have more muzzle energy at 40 yards than a 177 of equal power…a little but not to the extent anticipated
The closest I’ve found to accurate and retentive is what is now called the H&N Sniper
Dom,
Interesting. I could ask a bunch of questions on that statement , but will not. Interesting that you have in fact done down range chrony testing. Not something that you hear talked about often.
I will ask 1 question though….Do you use 1 chrony at muzzle and another at target, ( at the same time) OR… do you do an average at muzzle and then an average at target ( with the same chrony)?
One Chrony, and careful does it
It’s actually pretty fiddly and time consuming, but fascinating, you can go cross eyed at chairgun, or study the BC of the pellet all you want….the BC is a constant variable anyway…..I’m never quite sure what they mean when they give a figure…..it should be followed with “at 600 fps” or similar…..but it does throw up some results, I can’t remember all of my findings apart from the fact my 10.6 ft/lb HW35 was applying more energy (just) with a H&N FTT at 30 metres than my 11.5 ft/lb HW77 was with an RWS Superfield at the same distance……neither gun particularly likes FTT’s past about 25 metres though, which is fine
I’d like to mention that Chairgun adds another complication — it supports the use of 6 different profiles for the BC field; the default being one apparently optimized for some ideal pellet.
G1 is apparently an old standard for flat-based bullets — Google indicates there is also a G7 for boat-tail pointed…
The complication is that each of these profiles is based on a “standard projectile” and small changes from the standard to the actual can result in changes.
Chairgun also allows one to create a custom profile and use it.
Dom
I looked at PA’s new product page and they have those pellets in lite, medium and heavy weights now. I do like that pellet design which I call a dumbell design if you look at it.
I think that again as it goes that pellet design, weight and velocity are slk factors of how well a pellets energy is retained.
Some gun and pellet combinations might produce a ideal I guess I will say ballistic result and some gun and pellet combinations won’t produce a good result.
I think that’s where we fall back into that dreaded try a pellet and see what the results are in a given gun. And then also the retained energy matters more for different types of shooting your doing.
If the pellets getting down range accurately and it has the retained energy for the required job that gun and pellet does then that is a good combination. You need to know what you want that pellet to do.
Dom
You are 100% correct, the same is also true with firearms! In airguns, the velocity is limited by the powerplant, in firearms, by chamber pressure. As an example, in a 30-06, the most efficient bullet weight in my opinion is in the neighborhood of 165 grains.
I discovered another website, which I can’t mention here, I wanted to, but I already ran it by Edith and she said it wouldn’t fly. On it they test actual AG’s by make and model in the respective calibers for each. Once again as an example, lets look at the RWS model 48 in .177 caliber, the first air rifle I purchased last year. I do not know to what extent or how they do their testing, but they list the MV/FPE at the muzzle,10, 25 and 50 yards with over 30 different pellets (in .177 caliber)! Once you see it, you will see how quickly the the velocity and consequently FPE bleeds off with the lighter weight pellets, exactly the same with powder burners. This is why, in my opinion, that MV doesn’t mean squat! How many things do you shoot at the muzzle of a rifle? In the 48, at the muzzle, all the tested pellets have a FPE of 18-20 foot pounds with the exception of one which was too heavy for the powerplant. Of all these pellets, only four stood out at 50 yards, still carrying 10-12 foot pounds and none of them had 20 FPE at the muzzle!
At 50 yards, my 48 will blow a 7/32″ (.219″) hole through a piece of .135″ sheet lead with 10.34 grain JSB exact heavy and 10.65 grain H&N baracuda pellets. 10.5 Crosman ultra magnums will not penetrate it, but appear to be the most accurate so far.
Bugbuster
Check out this chart on the H & N Web site.
http://www.hn-sport.de/fileadmin/user_upload/pdf/service/Ballistischer_Koeffizient___Energiewerte/Englisch/Kaliber_5_5_EN.pdf.
would be nice if we had a lite pellet that could retain as much of it’s energy at 50yds as the Barracuda.
Pete
And know yourself too, if you aren’t accurate enough to group half inch at 30 yards with any pellet, then your hunting is restricted to 20 to 25 yards, which is where some pointeds and hollow points still hold accuracy, so a bit of realism can open up your pellet choice significantly, I use 177 to hunt at any sort of range, but would still grab a 22 and a tin of H&N Hollowpoints for ratting round farm buildings or squirrels, a good, resounding thwack at less than 25 yards, accuracy is fine too, push that out to 45 yards and they fly about all over the place…no good at all
I’m new to air guns. The word Diabolo is a bit confusing. I ordered the JSB Match Diabolo Test Sampler in 22 Cal. All the JSB;s are called Diabolo even though they have different shapes such as the Diabolo Exact Jumbo Monster 25.4 Grain.I was considering ordering the H&N Field Target Trophy 14.66 Grains in 22 Cal. But they are not called Diabolo Pellets . What is the difference? To look at them they are very similar in shape and size as the Diabolo Exact Jumbo Heavy 18.1 Gran, and the Diabolo Exact Jumbo RS 13.4 Grain. Any help would be appreciated.
Diabolo means wasp wasted or has an hourglass type shape.
The head is larger than the center and the skirt flares out from
the center.
Most modern pellets have the diabolo shape because it helps keep the pellet oriented correctly by using the air drag like a badminton birdie.
There are a few designs that don’t have this shape but personally I consider
those to be hollow bodied bullets.That’s my opinion and others may disagree.
Bill72,
JTinAL pretty much said it all. Diabolo is a generic term applied to all pellets that have the “wasp” shape. Proportion of head, waist and skirt will vary, but I think it’s fair to say that 95% of what is offered is Diabolo, Even if the ad or can does not say that.
Bill72,
Welcome to the blog.
Yes, the word diabolo is confusing. That’s because it is used in a couple different ways, without any standardization.
A diabolo is a type of juggling apparatus used around the world. It is a wheel that has a pinched center that is caught and thrown by a rope while the wheel is spinning. The pinched center was what pellet manufacturers keyed on when they first gave wasp-waisted pellets that name.
Diabolo means wasp-waisted with a hollow tail, when it refers to pellets. It’s a shape that guarantees the pellet will remain nose-forward in flight and also provides the least contact with the bore for reduced friction.
So a diabolo pellet isn’t a specific shape. It is a set of features — the wasp or pinched waist and the hollow tail.
But European pellet manufactures started very early using just the word diabolo when they meant pellet. Hence diabolo became a slang term for an airgun pellet. Most pellet makers use the term, but not all of them. That’s why you sometimes see it used and sometimes not.
Think of the term spitzer bullet. All it means is a pointed bullet. It doesn’t refer to a specific shape of bullet, other than the pointed nose. And spitzer is used as loosely as the term diabolo.
B.B.
BB,
Please, what brand of air compressor did you buy, the one you referred to as the best on the market?
AJ
I may be misremembering but I believe B.B. has this compressor
/product/freedom-f10-shoebox-electric-air-compressor-max-4500-psi?a=4899
So sorry to B.B. and others if I got this wrong.
JTinAL,
No, I do not own a Shoebox compressor.
B.B.
Whoops!! My bad,sorry for the mis-info.
Dang these senior moments are staring to run together.
AJ,
I do not remember the brand, but I believe BB bought a new one at a show awhile back. I do remember he said it was very quiet and about the size of a desk top’s “tower” unit. I think it was just under 3000$. So while he may have/still has a ShoeBox, I believe he “updated”.
AL,
I bought an Omega Super Charger. I wrote a feature article about it in Shotgun News and also in Airgun Hobbyist magazine. The Shotgun News article will be up on my website to read very soon.
http://www.thegodfatherofairguns.com
B.B.
B.B.,
It’s been up for 2 months.
Edith
Edith,
‘
Good to know. Our website is valuable, because I can put the things people often refer to there, and I always know where they are.
B.B.
AJ,
I uploaded the article about the Omega compressor to Tom’s site about 2 months ago.
Edith
Thank you Edith, found the article, will order one tomorrow.
AJ
Edith
How or why are strange posts/comments showing up on the “comments RSS” which are usually replys posted to Toms older blogs? This has been going on now for several days. I had never notice that before.
Bugbuster
Bugbuster
It’s spam .
My wife tells me that they get paid by how many spams they post, no matter where they post them .
They are also looking for word combinations that won’t get caught by spam filters.
twotalon
Twotalon
Thanks for the info, unfortunately, I am computer challenged and obviously don’t understand many of these things. It just caught my eye because they are becoming more and more frequent and had nothing to do with the blog.
Bugbuster
Bugbuster,
Those are spams that didn’t get caught by the spam filter. I look at the blog comments many times every day to search for those that get through and then remove them.
Edith
Edith
Thanks! I knew I should have hit the refresh icon before posting, got caught again! I don’t envy your job one bit, it has to be very trying.
Bugbuster
Bugbuster,
With a few exceptions, I’m permanently tired.
Edith
Edith
From all the great and sometimes tedious work that you do, you would have to be! You and Tom need a long vacation.
Bugbuster
Hi B.B.Pelletier, JTinAL, and Chris USA
Thanks for taking time out of your day to answer my question.
BB,
Based on you article, the BC of a pellet changes in flight as its velocity changes. Is this correct?
If so, it means the software that calculate pellet trajectory based also on a pellet’s BC is not that accurate. Is this correct?
The software may contain a profile (see my other post regarding Chairgun) with compensation factors for velocity. Based on a “standard projectile” so there will be errors if the projectile being modeled differs significantly.
The real question then becomes: what form factor was used to produce the base BC (and at what velocity the form factor is applied) [not applicable to air guns, but I just looked at the Sierra reloading manual, and they did give BCs at velocity points for each of their bullets… But, for example, most of the handgun bullets used one value all the way up to 1200fps, and then maybe a second value from 1200 to 1800fps, and a third value for over 1800fps; the rifle bullets tended to consider velocities up to 2000 fps as falling under one BC, then had two or three ranges up to 3000 or for some 4000 fps, and then one value over the top velocity]
While Chairgun appears to have ability to edit a custom profile, it doesn’t seem to allow loading a standard profile as a starting point. So I have no idea of what velocity they used for the BC@profile datum point.
Joe,
Something you and many others need to keep in mind is that Chairgun, reloading manuals, etc. get you into the ballpark. Each individual airgun, firearm, etc. will likely produce different results than the calculators, programs, charts, etc. will state. To determine what is the best pellet, best load, best projectile, ad infinitum requires individual experimentation. I for one have never used Chairgun. I have only used reloading manuals to provide me with a safe starting point.
Do not get hung up in the science of it all and miss out on the joy of it all. Get out there and shoot.
Joe,
Yes, the BC does change as the pellet flies downrange.
But the ballistic software does take this into account. They have algorithms that adjust for the BC in flight. I’m told they do get very close to reality.
The problem is with the shapes of the pellets. These must be guessed ay, or discovered by testing each pellet at multiple distances. Almost nobody takes the time to do that, so the shape factor is a good guess.
B.B.
BB,
Thanks, but which ballistic software do you recommend that is accurate?
Also where can I find the BC for my pellet for inputting into that ballistic software ?
Joe,
I don’t use any software. But Chairgun seems to be very good. As for the BC, you have to research and maybe test the pellet you are interested in.
B.B.
Chairgun comes with a “database” of pellets (though I think Chairgun 3 had more pellets listed than the current Chairgun 4). Main thing is: the price is right ($0, once one has registered on the website to get to the download page)
You’d have to pick the nearest matching pellet from the database and accept any inaccuracies due to variation…
Or you develop your own profile using a chronograph at distances out to whatever your limit is (at 100 yards, the odds are the dropping trajectory can’t cross over both sensors reliably). Going to be a lot of shooting, presuming a 10-shot average at each measurement distance… Chairgun does permit creating custom BC profiles (BC vs velocity) but I don’t know what velocity is then used for the database BC value.
Joe
That’s one of the things I talk about with Chairgun.
It is a estimation tool. There are to many factors involved to call a program a absolute.
Shoot and document results is always the best. That way you know what your gun and pellet is doing in real life situations.
BB,
I just read your article about the SSP pistol. I want one! I understand Daisy, but Crosman needs a boot in the backside! I would love to get my hands on the detailed plans for that thing.
RR
I agree as well they should have never stopped making it as it is by far better than any 2240 or 2400.
BD
Hatsans ?
Looking at getting into PCP’s. Looking at all brands. I would appreciate any comments (for) or (against) the Hatsan brand. (.22 or .25)
A few thoughts,… the P.A. sight does not recommend using the Weaver rail, but to use the 11mm. instead, as they say the Weaver rail is not a true Weaver rail.
Second, I believe they are a made in Turkey, and with all the upset in the mid-east, one has to wonder on future availability.
And last, I believe that one of our U.K. posters commented awhile back that the “used” market is full of Hatsans in the U.K.
Thanks, Chris
Chris, USA
I have a Hatsan AT44s10 long in 22 and it is a power house as it shoots in untouched from stock as follows
CPs 14.3s at1034fps for 34.02fpe
JSB 18.13s at 948 for 37.62fpe
H&N Barracuda 21.4s at 900fps for 39.19fpe
H&N FTT 16.26s at 994fps for 35.72fpe
Eley Magnum 30gr at 750 fps for 37.48 fpe this is a bullet shaper pellet that is no longer made
The new Predator PDG 26 grain pellet that is also a bullet shaped pellet at 860 fps for 42.71 fpe
I absolutely love this gun as it has given me no issues and it gets 35 to 40 shots per fill depending on the pellets and has a very flat curve. I have it sighted at 50 yards with the JSB 18.13s but I am going to resight with the predator PDG bullet shaped pellets since they give the most fpe and this is my hunting gun because it is such a powerhouse in stock form. I do not believe you will be disappointed in either 22 or 25 calibers.
BD
Buldawg76,
Awesome info. ! Notes will be made. Very nice to have actual data. The AT-44 or AT-65 is what I would consider (if) going with a Hatsan. While not sure, BB probably has done a review on one or both. If so, more data.
All options open at this point.
Thanks again, Chris
Chris, USA
I know for a fact that BB has done a review of the At44 s10 QE model that is suppressed from the factory , but I cannot say for sure if he has done one on the AT65 or not so him or Edith can give you the links to those reviews as I still have not become proficient at searching for the reviews or info on the blog yet as it is hit or miss for me with key words.
Mine is not the suppressed model and has the 23 inch barrel instead of the 19 inch that the QE uses so the shorter barrel will lessen the power some but by how much I cannot say but I wanted the longer barrel for the added power and since it is threaded on the end I do have a LDC on it so it is whisper quiet and it is made by hatsan for their guns.
I will not give you the info here on where to get it for a very reasonable price and they have 8 and ten inch long models and mine is the 8 inch and works very well although it does make the gun quite long as with it the barrel is 31 inches long total with the LDC.
I will send you info by email.
BD
Yup,….BB did a 5 part report on the AT-44,….I believe “put it on short list” was part of the conclusion. List updated.
Hi, folks. I wonder if any of you have any advice on a new scope for my Marauder Pistol carbine. This p-rod is meant for my eight- and 11-year old boys. The RAI adapter and UTG AR stock are terrific for instantly adjusting for smaller boy, larger boy, and overgrown dad-size boy. Right now, it wears an older Leapers 4-16×50 scope that I chose based on… it being available on my shelf. Love the Leapers, but it is a little heavy, and maybe a little big for this cute carbine.
Any wisdom here on something a little lighter and smaller? Emphasis on lighter, I think.
Some parameters: I do enjoy the occasional rat hunting, so maybe a bigger objective lens wouldn’t be the end of the world for those low-light rat shots? Especially since the p-rod needs a high-ish mount to clear its magazine, even with a small-ish objective. I also enjoy target-type turrets that I can click without removing caps. Also prefer etched reticles, and don’t mind illumination. Perhaps each of these parameters defeats the lightweight purpose, though?
Kevin, do you still advocate IIRC the smaller Burris Timberline?
Thanks,
Jan
PS, on the ballistic coefficient, I’m interested in that new Labradar chronograph. I hear it gives you velocity measures at several different ranges per shot. Seems ideal for conveniently measuring the BC with your ammo at your MV from your barrel…
A chronograph with the software built -in? Cool!
I received this from Andrew:
Hi, I’m looking for some info about an old air rifle all I know is it was bought new in the mid 60’s on the stock it a badge with jelly 5.5 the barrel is blocked with dust were it has sat in the cupboard for 40 ish years. have cock it and fire there is still a good kick to it. if anyone could tell me more about it I would love to be able to tell my uncle (the original purchaser) about it. kind regards Andy
Andrew,
I don’t answer private questions like this. I deal with 300-500 emails each day, and when there is a question others might benefit from, I answer it in the blog, which is where I am posting your question.
Your Jelly is really a Telly. The J is an odd font and is really a T.
Here is a 2-part report on a Relum Telly:
/blog/2012/12/the-relum-telly-part-2/
B.B.
B.B.,
Only you,..could turn “Jelly” into “Telly”,…that says something,….something really good.
😉
Chris,
That was a guest blog by Vince. He is no longer on the blog, but he was a great help to us all for many years.
B.B.
I look at eBay at this time and now a 1950’s Daisy Red Rider model 94 is at $181 + $22 shipping with 24 bids. The auction ends next Friday. Both the gun and box look like new in the pictures.
V8vega,
The 94 was a low-production Red Ryder. But that price is as high as it should go.
B.B.
Also on eBay until next Friday is a Crosman Pellgun 180 at $67 + 17. Seller says it works good and the pictures look good I didn’t know what it was until I googled it and Tom’s blog came up. Its a 22 CO2 that uses two powerlets with a velocity of 560 I think Tom said, pretty good for a CO2 22.
Tom mentioned the later version has a real good trigger. I didn’t go back to see how to tell but this one has a formed metal trigger guard it looks like.
V8vega,
The 180 is a one cartridge gun. Except that Montgomery Ward had Crosman build a special 180 model for them that was unlike any they made for others. That one does accept 2 cartridges. That would be a rare airgun.
B.B.